Funciones Exponenciales y Logarítmicas

    Las Funciones en nuestra Vida Cotidiana 

Las funciones en nuestra vida diaria son muy importantes ya que se van desarrollando poco a poco, en diferentes campos de la vida, por ejemplo tenemos a las funciones exponenciales que es conocida formalmente como la función real e^x, donde e es el número de Euler aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=e^x o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

Ejemplo 1

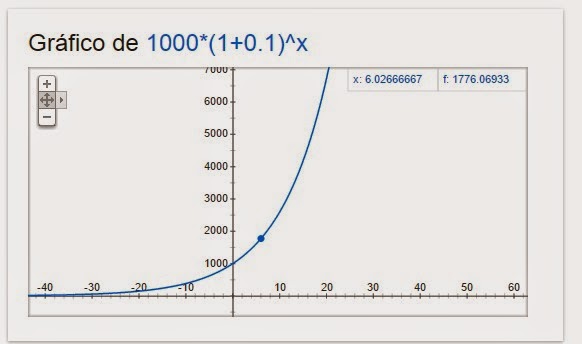
Un señor tiene depositados  en el banco 1,000 pesos. Lo invierte durante un periodo de 6 años con un interés del 10%. ¿Cuál será la cantidad de dinero que tendrá al finalizar su periodo?

R: f(t)=Ci(1+.1)^t

Donde: 

 t=tiempo transcurrido en años

Ci=Capital inicial

f(t)=1000(1.1)^6

f(t)=1000(1.771)

f(t)=1771

La cantidad de dinero que obtuvo al finalizar su periodo es de $1771

Ejemplo 2

Una  persona inventa un chisme, el número de personas que lo conocen actualmente es 1, pero si cada minuto se lo cuenta a otras 2, y esas 2 se lo cuentan a otras 2 cada una consecutivamente, el número de personas que conocerán el chisme abra ascendido de manera exponencial. ¿Cuántas personas estarán enterados del chisme al cabo de 10 minutos?

Una

R= la ecuación para resolverlo es la siguiente: f(x)=2^x

f(x)=2^10

f(x)=1024

Esto quiere decir que en 10 minutos 1024 personas sabrán el chisme inventado.

A continuación también tenemos las funciones logarítmicas que son aquellas que también  se reflejan por dichos acontecimientos en todo momento de la vida, en matemáticas, el logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. 

Una función logarítmica es aquella que genéricamente se expresa como f (x) = log_ax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

Esta unidad da a conocer los modelos funcionales que se rigen por las funciones exponenciales, la importancia que tiene éstos en la vida cotidiana y si observamos la función logarítmica como inversa de la función exponencial, comparáramos los modelos inversos que la conllevan.

Ejemplo 1

Ahora como podemos ver la función logarítmica es la inversa de la función exponencial. Esto se podrá observar con el problema anterior sobre el chisme: Una  persona inventa un chisme, el número de personas que lo conocen actualmente es 1, pero si cada minuto se lo cuenta a otras 2, y esas 2 se lo cuentan a otras 2 cada una consecutivamente, el número de personas que conocerán el chisme abra ascendido de manera exponencial. ¿En cuánto tiempo lo sabrán 1024 personas?

R= para resolver este problema se utiliza la función logarítmica.

 Dando como resultado x= 10, esto quiere decir que 1024 personas estarán esteradas en 10 min.

Ejemplo 2

Las estrellas se clasifican en categorías de brillo llamadas magnitudes. A las estrellas más débiles (con flujo luminoso   L0) se les asigna magnitud 6.  A las estrellas más brillantes se le asigna magnitud conforme a la fórmula: m = 6 − 2,5 · log( L L0 ).

En donde (L) es el flujo luminoso de las estrellas.

m: magnitudes = ?

LO: Flujo luminoso=6

L= Flujo luminoso de las estrellas maas brillantes.

a)      Determine m si L = 100,4 · L0.            

R: m=5.

b) Resuelve  la fórmula para evaluar L en términos de m y de  L0.        

      R: L = 10 6−m 2,5 L0.